Answer:
Explained below.
Explanation:
(11)
Subtract the sum of (13x - 4y + 7z) and (- 6z + 6x + 3y) from the sum of (6x - 4y - 4z) and (2x + 4y - 7z).
![[(6x - 4y - 4z) +(2x + 4y - 7z)]-[(13x - 4y + 7z) + (- 6z + 6x + 3y) ]\\=[6x-4y-4z+2x+4y-7z]-[13x-4y+7z-6z+6x+3y]\\=6x-4y-4z+2x+4y-7z-13x+4y-7z+6z-6x-3y\\=(6x+2x-13x-6x)+(4y-4y+4y-3y)-(4z+7z+7z-6z)\\=-11x+y-12z](https://img.qammunity.org/2021/formulas/mathematics/high-school/jrh5f8p34qle6jkgh5p6xy3tohtjglgvv5.png)
Thus, the final expression is (-11x + y - 12z).
(12)
From the sum of (x² + 3y² - 6xy), (2x² - y² + 8xy), (y² + 8) and (x² - 3xy) subtract (-3x² + 4y² - xy + x - y + 3).
![[(x^(2) + 3y^(2) - 6xy)+(2x^(2) - y^(2) + 8xy)+(y^(2) + 8)+(x^(2) - 3xy)] - [-3x^(2) + 4y^(2) - xy + x - y + 3]\\=[x^(2) + 3y^(2) - 6xy+2x^(2) - y^(2) + 8xy+y^(2) + 8+x^(2) - 3xy]- [-3x^(2) + 4y^(2) - xy + x - y + 3]\\=[4x^(2)+3y^(2)-xy+8]-[-3x^(2) + 4y^(2) - xy + x - y + 3]\\=4x^(2)+3y^(2)-xy+8+3x^(2)-4y^(2)+xy-x+y-3\\=7x^(2)-y^(2)-x+y+5](https://img.qammunity.org/2021/formulas/mathematics/high-school/cnf3jiqmoyns19p24uafy8rk83naxqkt7f.png)
Thus, the final expression is (7x² - y² - x + y + 5).
(13)
What should be subtracted from (x² – xy + y² – x + y + 3) to obtain (-x²+ 3y²- 4xy + 1)?
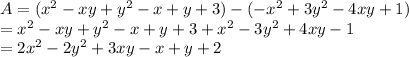
Thus, the expression is (2x² - 2y² + 3xy - x + y + 2).
(14)
What should be added to (xy – 3yz + 4zx) to get (4xy – 3zx + 4yz + 7)?
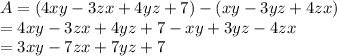
Thus, the expression is (3xy - 7zx + 7yz + 7).
(15)
How much is (x² − 2xy + 3y²) less than (2x² − 3y² + xy)?
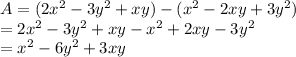
Thus, the expression is (x² - 6y² + 3xy).