Question

"For a first order instrument with a sensitivity of .4 mV/K and a time" constant of 25 ms, find the instrument’s response as a function of time for a sudden temperature increase from 273 K to 473 K. Before the temperature increase, the instrument output was a steady 109.2 mV. Plot the response y(t) as a function of time. What are the units for y(t)? Find the 90% rise time for y(t90) and the error fraction, Γ(t90).

Answer 1

Step-by-step explanation:

Given that:

For a first order instrument with a sensitivity of .4 mV/K

constant c = 25 ms = 25 × 10⁻³ s

The initial temperature
`T_1` = 273 K

The final temperature
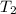`T_2` = 473 K

The initial volume = 0.4 mV/K × 273 K = 109.2 V

The final volume = 0.4 mV/K × 473 K = 189.2 V

the instrument’s response as a function of time for a sudden temperature increase can be computed as follows:

Let consider y to be the function of time i.e y(t).

So;

y(t) = 109.2 + (189.2 - 109.2)( 1 -
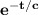`\mathbf{e^(-t/c)}`)mV

y(t) = (109.2 + 80 ( 1 -
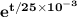`\mathbf{e^{t/25* 10^(-3)}}`)) mV

Plot the response y(t) as a function of time.

The plot of y(t) as a function of time can be seen in the diagram attached below.

What are the units for y(t)?

The unit for y(t) is mV.

Find the 90% rise time for y(t90) and the error fraction,

The 90% rise time for y(t90) is as follows:

Initially 90% of 189.2 mV = 0.9 × 189.2 mV

= 170.28 mV

170.28 mV = (109.2 + 80 ( 1 -
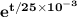`\mathbf{e^{t/25* 10^(-3)}}`)) mV

170.28 mV - 109.2 mV = 80 ( 1 -
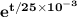`\mathbf{e^{t/25* 10^(-3)}}`)) mV

61.08 mV = 80 ( 1 -
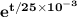`\mathbf{e^{t/25* 10^(-3)}}`)) mV

0.7635 mV = ( 1 -
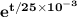`\mathbf{e^{t/25* 10^(-3)}}`)) mV

t = 1.44 × 25 × 10⁻³ s

t = 0.036 s

t = 36 ms

The error fraction =
`(189.2-170.28 )/(189.2)`

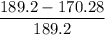
The error fraction = 0.1

The error fraction = 10%