Question

A 0.500 H inductor is connected in series with a 93 Ω resistor and an ac source. The voltage across the inductor is V = −(11.0V)sin[(500rad/s)t]. What is the voltage across the resistor at 2.09 x 10-3 s? Group of answer choices 205 V 515 V 636 V 542 V

Answer 1

205 V

V
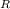`_(R)` = 2.05 V

Step-by-step explanation:

L = Inductance in Henries, (H) = 0.500 H

resistor is of 93 Ω so R = 93 Ω

The voltage across the inductor is

`V_(L) = - IwLsin(wt)`

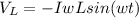
w = 500 rad/s

IwL = 11.0 V

Current:

I = 11.0 V / wL

= 11.0 V / 500 rad/s (0.500 H)

= 11.0 / 250

I = 0.044 A

Now

V
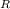`_(R)` = IR

= (0.044 A) (93 Ω)

V
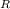`_(R)` = 4.092 V

Deriving formula for voltage across the resistor

The derivative of sin is cos

V
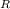`_(R)` = V
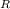`_(R)` cos (wt)

Putting V
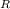`_(R)` = 4.092 V and w = 500 rad/s

V
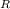`_(R)` = V
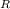`_(R)` cos (wt)

= (4.092 V) (cos(500 rad/s )t)

So the voltage across the resistor at 2.09 x 10-3 s is which means

t = 2.09 x 10⁻³

V
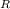`_(R)` = (4.092 V) (cos (500 rads/s)(2.09 x 10⁻³s))

= (4.092 V) (cos (500 rads/s)(0.00209))

= (4.092 V) (cos(1.045))

= (4.092 V)(0.501902)

= 2.053783

V
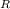`_(R)` = 2.05 V