Question

A city is holding a referendum on increasing property taxes to pay for a new high school. In a survey of 434 likely voters, 202 said that they would vote "yes" on the referendum. Create a 95% confidence interval for the proportion of likely voters who would vote "yes" on the referendum. Use a TI-83, TI-83 plus, or TI-84 calculator, rounding your answers to three decimal places.

Answer 1

Answer: 0.418 < p < 0.512

Step-by-step explanation: A 95% conifdence interval for a population proportion is given by:

`p + z\sqrt{(p(1-p))/(n) }`

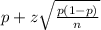
where:

p is the proportion

z is score in z-table

n is sample size

The proportion for people who said "yes" is

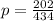`p=(202)/(434)` = 0.465

For a 95% confidence interval, z = 1.96.

Calculating

`0.465 + 1.96*\sqrt{(0.465(0.535))/(434) }`

`0.465 + 1.96*√(0.00057)`

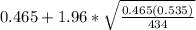
0.465 ± 1.96*0.024

0.465 ± 0.047

Interval is between:

0.465 - 0.047 = 0.418

0.465 + 0.047 = 0.512

The interval with 95% of confidence is between 0.418 and 0.512.