Question

A researcher wishes to estimate the percentage of adults who support abolishing the penny. What size sample should be obtained if he wishes the estimate to be within 3 percentage points with 99​% confidence if ​(a) he uses a previous estimate of 22​%?

Answer 1

Sample size n
`\simeq` 1269.15

Explanation:

From the information given ,

At 99% of confidence interval,

the level of significance ∝ = 1 - 0.99

the level of significance ∝ = 0.01

the critical value for 99% of confidence interval is:

`\mathtt{(\alpha )/(2) = (0.01)/(2)}`

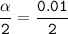
= 0.005

`\mathtt {z_(\alpha/2) = z_(0.005/2) }`

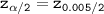
The value for z from the standard normal tables

= 2.58

The Margin of error E= 3% = 0.03

The formula to determine the sample size n used can be expressed as follows:

`\mathtt { n = ((z_(\alpha/2))/(E))^2 \ \hat p (1 - \hat p) }`

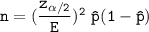
where;

`\mathtt{\hat p }` = 22% = 0.22

Then:

`\mathtt { n = ((2.58)/(0.03))^2 \ * 0.22 * (1 - 0.22) }`

`\mathtt { n = (86)^2 \ * 0.22 * (0.78) }`

`\mathtt { n = 7396 \ * 0.22 * (0.78) }`

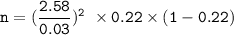
n = 1269.1536

Sample size n
`\simeq` 1269.15