Answer:
Sample size n
 1269.15
1269.15
Explanation:
From the information given ,
At 99% of confidence interval,
the level of significance ∝ = 1 - 0.99
the level of significance ∝ = 0.01
the critical value for 99% of confidence interval is:
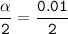
= 0.005
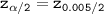
The value for z from the standard normal tables
= 2.58
The Margin of error E= 3% = 0.03
The formula to determine the sample size n used can be expressed as follows:
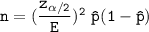
where;
 = 22% = 0.22
= 22% = 0.22
Then:
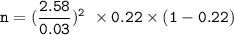
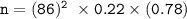
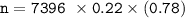
n = 1269.1536
Sample size n
 1269.15
1269.15