Question

If 0≤β<2π, find all values of β that satisfy the equation cos(2β)=√3/2

Answer 1

He’s right^ the dude above me has the right answer

Answer 2

π/12 rad and 23π/12 rad

Explanation:

Given the expression cos(2β)=√3/2 for 0≤β<2π, we are to find the value of β within the range that satisfies the equation.

`cos(2\beta)=√( 3)/2\\\\take \ the\ arccos\ of \ both \ sides\\\\cos^(-1)cos(2\beta) = cos^(-1)\sqrt{{3} }/2 \\ \\2\beta = cos^(-1)\sqrt{{3} }/2 \\\\2\beta = 30^0\\\\\beta = 30/2\\\\\beta = 15^0`

Since cos id positive in the 4th quadrant,
`\beta = 360^0-15^0`,
`\beta = 345^0`

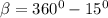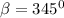
Hence the value of
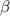`\beta` that satisfy the equation are 15° and 345°

Converting to radians;

180° = πrad

15° = 15π/180 rad

15° = π/12 rad

345° = 345π/180

345° = 23π/12 rad

The values in radians are π/12 rad and 23π/12 rad