Answer:
D.
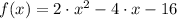
Explanation:
Any parabola is modelled by a second-order polynomial, whose standard form is:

Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 ,
,
 ,
,
 - Coefficients, dimensionless.
- Coefficients, dimensionless.
In addition, a system of three linear equations is constructed by using all known inputs:
(-2, 0)
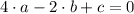 (Eq. 1)
(Eq. 1)
(4, 0)
 (Eq. 2)
(Eq. 2)
(0,-16)
 (Eq. 3)
(Eq. 3)
Then,
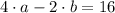 (Eq. 4)
(Eq. 4)
 (Eq. 5)
(Eq. 5)
(Eq. 3 in Eqs. 1 - 2)
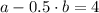 By Eq. 4 (Eq. 4b)
By Eq. 4 (Eq. 4b)
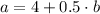
Then,
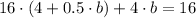 (Eq. 4b in Eq. 5)
(Eq. 4b in Eq. 5)
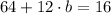

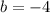
The remaining coeffcient is:
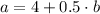
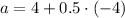
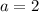
The function that represents a parabola with zeroes at x = -2 and x = 4 and y-intercept (0,16) is
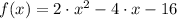 . Thus, the right answer is D.
. Thus, the right answer is D.