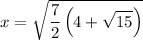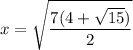Question

If


`√(5) x = √(3) x + √(7)`
find the value of x in the form

`\sqrt{ (a)/(b) }`
​

Answer 1

x= 7/4 x 25/6 is the answer

Answer 2

`$x=\sqrt{(7(4+√(15)))/(2)} $`

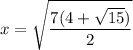
Explanation:

From the way it is written, the
`x` is outside the square root. I will rewrite it as:

`x√(5) =x√(3) +√(7)`

`x√(5)-x√(3)=√(7)`

`x(√(5) - √(3) )=√(7)`

`$x= (√(7) )/(√(5) - √(3)) \implies (√(7)(√(5) + √(3)) )/(2) $`

`$x=(1)/(2) √(7) (√(5) + √(3) )$`

`$x=(√(35))/(2) +( √(21))/(2) $`

`$x=(√(35)+√(21))/(2) $`

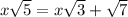
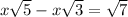
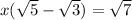
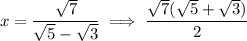
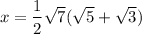
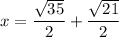
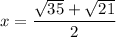
Multiply denominator and numerator by 3

`$x=(3√(35)+3 √(21))/(6) $`

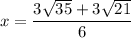
Factor
`√(3)`

`√(3) (√(105)+3 √(7))`

`$x=(√(3) (√(105)+3 √(7)))/(6) $`

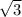
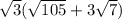
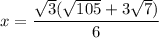
Divide denominator and numerator by
`√(3)`

`$x=(√(105)+3 √(7))/(2√(3) ) $`

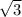
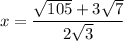
Let's rewrite it again

`$x=\frac{\sqrt{ (√(105)+3 √(7))^2}}{√(12) } $`

`$x=\sqrt{ (1)/(12) \cdot (√(105)+3 √(7))^2}$`

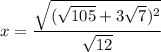
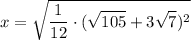
It is already in the form
`$\sqrt{(a)/(b) } $`

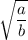
Expanding the perfect square, we have

`63+42√(15)+105`

`$(63)/(12) +(42√(15))/(12) +(105)/(12) $`

`$(21)/(4) +(7√(15))/(2) +(35)/(4) $`

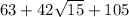
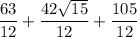
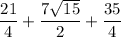
Factor
`$(7)/(2) $`

`$(7)/(2) (4+√(15) )$`

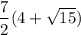
Therefore,

`$x=\sqrt{(7)/(2) \left(4+√(15) \right)} $`

`$x=\sqrt{(7(4+√(15)))/(2)} $`