Answer:
(A) 0.11
(B) 0.0526
(C) Related
(D) 0.28
Explanation:
The data provided is:
DC = event that a randomly selected driver is using a cell phone
TA = event that a randomly selected driver has a traffic accident
(A)
From the provided data:
P (DC) = 0.11
(B)
From the provided data:
P (TA) = 0.0526
(C)
To determine whether the events DC and TA are dependent, we need to show that:
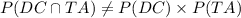
The value of P (DC ∩ TA) is,
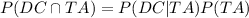
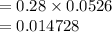
Now compute the value of P (DC) × P (TA) as follows:
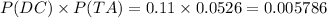
So,
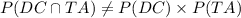
Thus, cell phone use while driving and traffic accidents are related.
(D)
The probability that the driver was distracted by a cell phone given that the driver has an accident is:
P (DC | TA) = 0.28