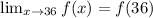Answer:
The function is continuous at x = 36
Explanation:
From the question we are told that
The function is
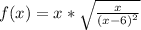
The point at which continuity is tested is x = 1
Now from the definition of continuity ,
At function is continuous at k if only
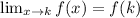
So
![\lim_(x \to 36)f(x) = \lim_(n \to 36)[x * \sqrt{ (x)/( (x-6) ^2 ) }]](https://img.qammunity.org/2021/formulas/mathematics/college/ult578mcnh8uj8ug0u3ssih9omojwakpn3.png)
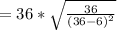
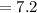
Now
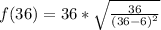
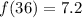
So the given function is continuous at x = 36
because