Question

Timothy invested $2,000 in an account earning 3.5% annual interest that is compounded continuously. How long will it take the investment to grow to $3,500?

Answer 1

Answer: 16 years

Explanation:

The exponential function for continuous growth is given by :-

`P=Ae^(rt)`

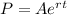
, where A = initial amount, r= rate of growth and t = time.

As per given , we have

A= $2,000, =r 3.5%=0.035 and P= $3500

put these vales in equation , we get

`3500=2000e^(0.035t)\\\\\Rightarrow\ (3500)/(2000)=e^(0.035t)\\\\\Rightarrow\ 1.75=e^(0.035t)`

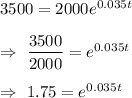
Taking log on both sides , we get

`\ln 1.75=0.035t\\\\\Rightarrow\ t=(\ln1.75)/(0.035)=(0.560)/(0.035)=16`

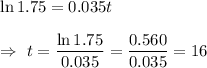
Hence, it will take 16 years to grow to $3,500.