Answer: ABCD is a parallelogram.
Explanation:
First we plot these point on a graph as given in attachment.
From the attachment we can observe that AD || BC || x-axis .
also, AB ||CD, that will make ABCD a parallelogram , but to confirm we check the property of parallelogram "diagonals bisect each other" , i.e . "Mid point of both diagonals are equal".
Mid point of AC=
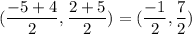
Mid point of BD=
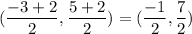
Thus, Mid point of AC=Mid point of BD
i.e. diagonals bisect each other.
That means ABCD is a parallelogram.