Question

1. Draw the graph of f(x) = cos x for 0 I know how to construct the graph but I don’t know how to get the figures. Please help

Answer 1

Please refer to the attached figure.

Explanation:

Given the function:

`f(x) =cosx \ where\ \{0^\circ\leq x\leq 360^\circ\}`

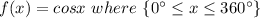
OR, the given function can also be written as:

`y = f(x) = cosx`

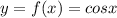
We know that graph of cosine is a wave.

and the range of cosine function is [-1, 1]

First of all, let us have a table of values at major values of x.

`x = 0, f(x) = 1\\x = 90, f(x) = 0\\x = 180, f(x) = -1\\x = 270, f(x) = 0\\x = 360, f(x) = 1`

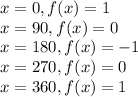
So, the table of values for f(x) is:

`\begin{center}\begin{tabular}{ c c }x & cosx \\0 & 1 \\90 & 0\\180 & -1\\270 & 0\\360 & 1\\\end{tabular}\end{center}`

Let us mark these points on the xy coordinate axis where x axis represents value of x and y axis represents value of
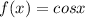`f(x) = cosx` and then join the points using a wave.

Please refer to the attached graph for the answer image.