Question

What is the radius for a circle whose equation is x2 + y2 = 64

Answer 1

radius of 8

Explanation:

step one :

Given that the equation of the circle is described as

`x^2 + y^2 = 64`

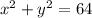
To correctly identify the center of the circle we have to place the equation in the standard form.

the standard equation for a circle is

`(x-h)^2+(x-k)^2= r^2`

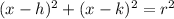
step two :

let us re-write the given equation so that we can compare it with the general equation of circle

`(x-0)^2+(x-0)^2= 8^2`

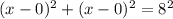
step three:

From this above equation in step two we can see that the circle has a radius of 8