Question

Determine the formula for the nth term of the sequence:
-2,1,7,25,79,...​

Answer 1

A plausible guess might be that the sequence is formed by a degree-4* polynomial,

`x_n = a n^4 + b n^3 + c n^2 + d n + e`

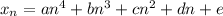
From the given known values of the sequence, we have

`\begin{cases}a+b+c+d+e = -2 \\ 16 a + 8 b + 4 c + 2 d + e = 1 \\ 81 a + 27 b + 9 c + 3 d + e = 7 \\ 256 a + 64 b + 16 c + 4 d + e = 25 \\ 625 a + 125 b + 25 c + 5 d + e = 79\end{cases}`

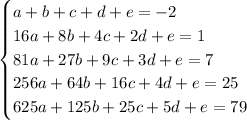
Solving the system yields coefficients

`a=\frac58, b=-\frac{19}4, c=\frac{115}8, d = -\frac{65}4, e=4`

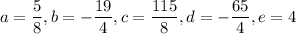
so that the n-th term in the sequence might be

`\displaystyle x_n = \boxed{(5 n^4)/(8)-(19 n^3)/(4)+(115 n^2)/(8)-(65 n)/(4)+4}`

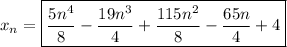
Then the next few terms in the sequence could very well be

`\{-2, 1, 7, 25, 79, 208, 466, 922, 1660, 2779, \ldots\}`

It would be much easier to confirm this had the given sequence provided just one more term...

* Why degree-4? This rests on the assumption that the higher-order forward differences of
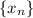`\{x_n\}` eventually form a constant sequence. But we only have enough information to find one term in the sequence of 4th-order differences. Denote the k-th-order forward differences of
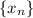`\{x_n\}` by
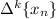`\Delta^(k)\{x_n\}`. Then

• 1st-order differences:

`\Delta\{x_n\} = \{1-(-2), 7-1, 25-7, 79-25,\ldots\} = \{3,6,18,54,\ldots\}`

• 2nd-order differences:

`\Delta^2\{x_n\} = \{6-3,18-6,54-18,\ldots\} = \{3,12,36,\ldots\}`

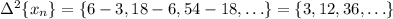
• 3rd-order differences:

`\Delta^3\{x_n\} = \{12-3, 36-12,\ldots\} = \{9,24,\ldots\}`

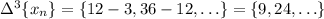
• 4th-order differences:

`\Delta^4\{x_n\} = \{24-9,\ldots\} = \{15,\ldots\}`

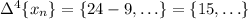
From here I made the assumption that
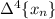`\Delta^4\{x_n\}` is the constant sequence {15, 15, 15, …}. This implies
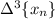`\Delta^3\{x_n\}` forms an arithmetic/linear sequence, which implies
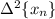`\Delta^2\{x_n\}` forms a quadratic sequence, and so on up
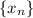`\{x_n\}` forming a quartic sequence. Then we can use the method of undetermined coefficients to find it.