Question

In an examination ,80%examines passed in english,70%In mathematics and 60% in both subjects.if 45 examines failed in both subject.

1.draw a venn-diagram to represent the above information .
2.find the number of examines who passed only one subject.
3.find the number of student who failed in mathematics.​

Answer 1

1. Please refer to attached diagram.

2. 135

3. 135

Explanation:

Given that

80%examines passed in English, n(E) = 80%

70%In mathematics, n(M) = 70%

and 60% in both subjects, n(E
`\cap` M) = 60%

45 examines failed in both subject.

1. Venn Diagram is attached in the answer area.

One circle represents the pass examines in Maths and

Other circle represents the pass examines in English.

Rectangle represents the total number of examines that appeared for the exam.

Rectangle minus the area of union of circles represent the number of students who failed in both subjects.

2. To find the number of examines who passed in only one subject.

i.e. n(E) - n(E
`\cap` M) + n(M) - n(E
`\cap` M) = (80 - 60 + 70 - 60)% = 30%

Let us find the number of students who passed in atleast one subject:

`n(E\cup M) = n(E) +n(M)-n(E \cap M)\\\Rightarrow n(E\cup M) = (80 +70-60)\% = \bold{90\%}`

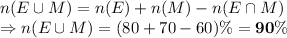
So, number of students who failed in both subjects = 100 - 90% = 10% of total students = 45

So, total number of students appeared = 450

So, number of examines who passed in only one subject = 450
`*` 30% = 135

3. Number of students who failed in mathematics.

100% - Passed in Mathematics = 100% - 70% = 30% of 450 = 135