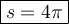Answer:
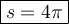
Explanation:
The arc length is determined by the formula
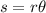 , where s is the arc length, r is the radius, and
, where s is the arc length, r is the radius, and
 is the value of the central angle (in radian formatting).
is the value of the central angle (in radian formatting).
By substituting the values for the radius and the central angle, you can solve for the arc length.
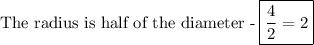 .
.
The central angle is converted to radian form by multiplying the angle in degrees by the fraction of π/180 - 360° * π/180 = 360π/180 = 2π.
Now, substitute the values and solve for s.
s = (2)(2π)