Answer:
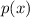 and
and
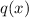 have the same domain and the same range.
have the same domain and the same range.
Explanation:
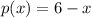 and
and
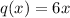
First of all, let us have a look at the definition of domain and range.
Domain of a function
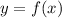 is the set of input value i.e. the value of
is the set of input value i.e. the value of
 for which the function
for which the function
 is defined.
is defined.
Range of a function
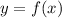 is the set of output value i.e. the value of
is the set of output value i.e. the value of
 or
or
 for the values of
for the values of
 in the domain.
in the domain.
Now, let us consider the given functions one by one:
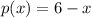
Let us sketch the graph of given function.
Please find attached graph.
There are no values of
 for which p(x) is not defined so domain is All real numbers.
for which p(x) is not defined so domain is All real numbers.
So, domain is
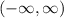 or
or
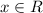
Its range is also All Real Numbers
So, Range is
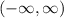 or
or
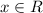
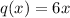
Let us sketch the graph of given function.
Please find attached graph.
There are no values of
 for which
for which
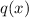 is not defined so domain is All real numbers.
is not defined so domain is All real numbers.
So, domain is
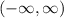 or
or
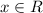
Its range is also All Real Numbers
So, Range is
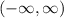 or
or
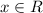
Hence, the correct answer is:
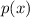 and
and
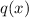 have the same domain and the same range.
have the same domain and the same range.