Question

According to the U.S. Energy Information Administration the average number of televisions per household in the United States was 2.3. A college student claims the average number of TV’s per household in the United States is different. He obtains a random sample of 73 households and finds the mean number of TV’s to be 2.1 with a standard deviation of 0.84. Test the student’s claim at the 0.01 significance level.

Answer 1

Answer with explanation:

Let
`\mu` be the average number of televisions per household in the United States .

As per given ,

`H_0:\mu =2.3\\\\ H_a:\mu\\eq2.3`

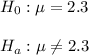
Since
`H_a` is two-tailed and population standard deviation is unknown, so the test is two-tailed t-test.

For sample : Sample size : n= 73, sample mean:
`\overline{x}` = 2.1, sample standard deviation : s= 0.84.

`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

`t=(2.1-2.3)/((0.84)/(√(73)))\\\\ t=-2.034`

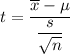
T-critical value for degree of freedom n-1 = 73-1=72 and 0.01 significance level is 2.646 . [By students' t-distribution table]

Since,
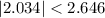`|2.034|<2.646` i.e.
`|T_(cal)|<|T_(crit)|`

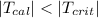
This means we cannot reject null hypothesis.

We conclude that the average number of televisions per household in the United States is 2.3 at the 0.01 significance level.