Answer:
The lines DE and BC have the same slope, therefore the two lines, DE and BC, are parallel
Explanation:
To prove that DE is parallel to BC, we have;
The slope, m of the lines DE and BC are found from the following equation;
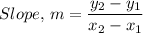
Where;
(x₁, y₁) and (x₂, y₂) = (b, c) and (a + b + c) for DE, we have;
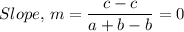
Where we have (x₁, y₁) and (x₂, y₂) = (0, 0) and (2a, 0) for BC, we have;
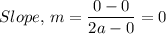
Therefore, because the lines DE and BC have the same slope, the two lines DE and BC are parallel.