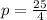Question

Find the constant $p$ such that $x^2 - 5x + p$ is the square of a binomial.

Answer 1

`p = (25)/(4)`

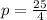
Explanation:

Given

`x\² - 5x + p`

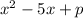
Required

Find p, such that the expression is a perfect square

Write out the coefficient of x

Coefficient = -5

Next step is to divide the coefficient of x by 2

`Result = \½(-5)`

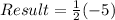
Take the square of the above expression to give p

`p = (\½(-5))\²`

`p = (\½(-5) * (\½(-5)`

`p = \½ * \½ * (-5) * (-5)`

`p = \¼(25)`

`p = (25)/(4)`

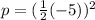
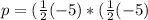
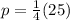
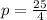
Substitute 25/4 for p in the given expression

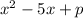`x\² - 5x + p` becomes

`x\² -5x + (25)/(4)`

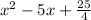
Expand the above expression

`x\² - (5x)/(2) - (5x)/(2) + (25)/(4)`

Factorize

`x(x - (5)/(2)) - (5)/(2)(x - (5)/(2))`

`(x - (5)/(2))(x - (5)/(2))`

`(x - (5)/(2))\²`

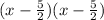
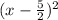
Hence, the value of p is
`p = (25)/(4)`