Question

Please help me out!!! There’s 25 questions I can’t

Answer 1

Explanation -:

In this question we are provided with the height and radius. We are asked to calculate the volume of a composite solid

First we will find the volume of a cone

We know,

`\orange{\star \: \small\boxed{ \sf{ Volume_((cone)) = (1)/(3)πr²h}}}`

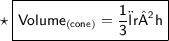
Where,

• r stand for radius
• h stand for height
• Assuming π as 3.14

Substituting the values we get

`\small\bf Volume_((cone)) = (1)/(3) * 3.14×4 × 4×5`

`\rightarrow \small\rm{ Volume_((cone)) = (1)/(3)×251.2}`

`\small\sf{ Volume_((cone)) = 83.73 \:cubic \: units }`

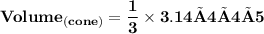
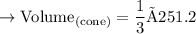
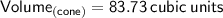
Now we will calculate the volume of a hemisphere

We know,

`\red{\star \: \small \boxed{\sf{ Volume_((hemisphere)) = (2)/(3)πr³}}}`

Substituting the values we get

`\small\bf{ Volume_((hemisphere)) = (2)/(3) * 3.14 × 4 × 4 × 4}`

`\rightarrow\small\rm{ Volume_((hemisphere)) = (2)/(3) * 200.96}`

`\rightarrow\small\rm{Volume_((hemisphere)) = 2 * 66.98}`

`\small\sf{ Volume_((hemisphere)) =133.97}`

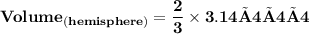
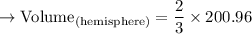
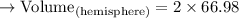
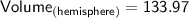
Now we will calculate the volume

Volume = 83.73 + 133.97 = 217.70 cubic units

Answer 2

217.70 cubic units

Explanation:

Volume of composite solid

Cone:

h= 5 units & r = 4 units

`\sf \boxed{Volume \ of \ cone = (1)/(3) \pi r^2h}`

`\sf = (1)/(3)*3.14*4*4*5\\\\ = 83.73 \ cubic units`

Hemisphere:

r = 4 units

`\sf \boxed{Volume \ of \ hemisphere = (2)/(3) \pi r^3}`

`\sf = (2)/(3)*3.14*4*4*4\\\\= 133.97 \ cubicunits`

Volume of composite solid = 83.73 + 133.97

= 217.70 cubic units