Answer:
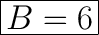
Explanation:
They are two way to solution.
METHOD 1:
Factor the polynomial on the left side of the equation:
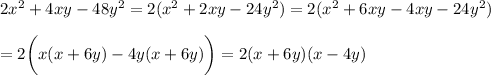
Therefore:
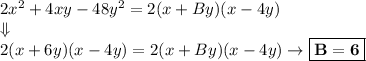
METHOD 2:
Multiply everything on the right side of the equation using the distributive property and FOIL:
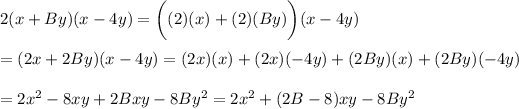
Compare polynomials:
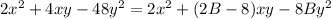
From here we have two equations:
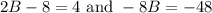
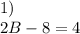 add 8 to both sides
add 8 to both sides
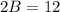 divide both sides by 2
divide both sides by 2
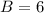
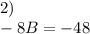 divide both sides by (-8)
divide both sides by (-8)
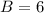
The results are the same. Therefore B = 6.