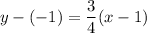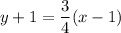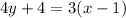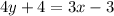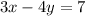Answer:
C) 3x - 4y = 7
Explanation:
The midpoint of AB is
M( (-2 + 4)/2, (-5 + 3)/2 ) = M(1, -1)
Line AB has slope:
(3 - (-5))/(-2 - 4) = 8/(-6) = -4/3
Slopes of perpendicular lines are negative reciprocals.
A perpendicular to line AB has slope 3/4.
The perpendicular to line AB that passes through the midpoint of segment AB is the line we want.