Answer:
b ≈ 9.2
Explanation:
Using Pythagoras' identity in the right triangle.
The square on the hypotenuse is equal to the sum of the squares on the other 2 sides, that is
b² = a² + c² = 6² +7² = 36 + 49 = 85 ( take the square root of both sides )
b =
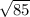 ≈ 9.2 ( to the nearest tenth )
≈ 9.2 ( to the nearest tenth )