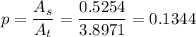Question

Let $DEF$ be an equilateral triangle with side length $3.$ At random, a point $G$ is chosen inside the triangle. Compute the probability that the length $DG$ is less than or equal to $1.$

Answer 1

13.44%

Explanation:

For DG to have length of 1 or less, point G must be contained in a sector of a circle with center at point D, radius of 1, and a central angle of 60°.

The area of that sector is

`A_s = (n)/(360^\circ)\pi r^2`

`A_s = (60^\circ)/(360^\circ) * 3.14159 * 1^2`

`A_s = 0.5254`

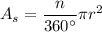
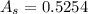
The area of the triangle is

`A_t = (1)/(2)ef \sin D`

`A_t = (1)/(2)* 3 * 3 \sin 60^\circ`

`A_t = 3.8971`

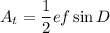
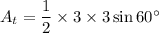
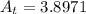
The probability is the area of the sector divided by the area of the triangle.

`p = (A_s)/(A_t) = (0.5254)/(3.8971) = 0.1344`

Answer 2

`|\Omega|=(\text{the area of the triangle})=(a^2\sqrt3)/(4)=(3^2\sqrt3)/(4)=(9\sqrt3)/(4)\\|A|=(\text{the area of the sector})=(\alpha\pi r^2)/(360)=(60\pi \cdot 1^2)/(360)=(\pi)/(6)\\\\\\P(A)=((\pi)/(6))/((9\sqrt3)/(4))\\\\P(A)=(\pi)/(6)\cdot(4)/(9\sqrt3)\\\\P(A)=(2\pi)/(27\sqrt3)\\\\P(A)=(2\pi\sqrt3)/(27\cdot3)\\\\P(A)=(2\pi\sqrt3)/(81)\approx13.4\%`