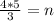Question

If n is directly proportional to the cube of mand n = 27 when m=

the value of n when m= 2.
(ii) the value of m
when n = 125​

Answer 1

Missing Part of the Question

If n is directly proportional to the cube of m and n = 27 when m = 4

Answer:

i.
`n = (27)/(64)`

ii.
`n = (20)/(3)`

Step-by-step explanation:

Given

Direct proportion between n and cube of m

This is represented as:

`n\ \alpha\ m^3`

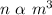
Convert proportion to equation

`n = km^3`

Where k is the constant of variation;

Substitute 27 for n and 4 for m

`27 = k * 4^3`

`27 = k * 64`

`27 = 64k`

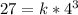
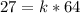
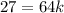
Divide both sides by 64

`k = (27)/(64)`

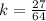
Solving for n when m = 2.

Recall that
`n = km^3`

Substitute
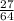`(27)/(64)` for k and 2 for m

`n = (27)/(64) * 2^3`

`n = (27)/(64) * 8`

`n = (27 * 8)/(64)`

`n = (27)/(64)`

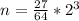
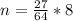
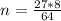
Solving for the value of m when n = 125​

Recall that
`n = km^3`

Substitute 125 for n and
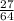`(27)/(64)` for k

`125 = (27)/(64) * n^3`

`125 = (27 * n^3)/(64)`

`125 = (27 n^3)/(64)`

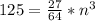
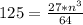
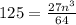
Multiply both sides by 64

`64 * 125 = (27 n^3)/(64) * 64`

`64 * 125 = 27 n^3`

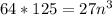
Divide both sides by 27

`(64 * 125)/(27) = (27n^3)/(27)`

`(64 * 125)/(27) =n^3`

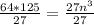
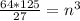
Take Cube root of both sides

`\sqrt[3]{(64 * 125)/(27)} = \sqrt[3]{n^3}`

`\sqrt[3]{(64 * 125)/(27)} = n`

`(4 * 5)/(3) = n`

`(20)/(3) = n`

`n = (20)/(3)`