Question

Find a cubic polynomial with integer coefficients that has $\sqrt[3]{2} + \sqrt[3]{4}$ as a root.

Answer 1

`y^3 -6y-6`

Answer 2

Find the powers
`a=√(2)+√(3)`

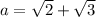
$a^{2}=5+2 \sqrt{6}$

$a^{3}=11 \sqrt{2}+9 \sqrt{3}$

The cubic term gives us a clue, we can use a linear combination to eliminate the root 3 term $a^{3}-9 a=2 \sqrt{2}$ Square $\left(a^{3}-9 a\right)^{2}=8$ which gives one solution. Expand we have $a^{6}-18 a^{4}-81 a^{2}=8$ Hence the polynomial $x^{6}-18 x^{4}-81 x^{2}-8$ will have a as a solution.

Note this is not the simplest solution as $x^{6}-18 x^{4}-81 x^{2}-8=\left(x^{2}-8\right)\left(x^{4}-10 x^{2}+1\right)$

so fits with the other answers.