Question

Please give me the answer ASAP The average of 5 numbers is 7. If one of the five numbers is removed, the average of the four remaining numbers is 6. What is the value of the number that was removed Show Your Work

Answer 1

Okay, let's slightly generalize this

Average of
`n` numbers is
`a`

and then
`r` numbers are removed, and you're asked to find the sum of these
`r` numbers.

Solution:

If average of
`n` numbers is
`a` then the sum of all these numbers is
`n\cdot a`

Now we remove
`r` numbers, so we're left with
`(n-r)` numbers. and their. average will be
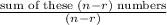`{\text{sum of these } (n-r) \text{ numbers} \over (n-r)}` let's call this new average
`a^(\prime)`

For simplicity, say, sum of these
`r` numbers, which are removed is denoted by
`x` .

so the new average is
`\frac{\text{Sum of } n \text{ numbers} - x}{n-r}=a^(\prime)`

or,
`(n\cdot a -x)/(n-r)=a^(\prime)`

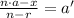
Simplify the equation, and solve for
`x` to get,

`x= n\cdot a -a^(\prime)(n-r)=n(a-a^(\prime))+ra^(\prime)`

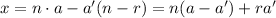
Hope you understand it :)

Answer 2

The removed number is 11.

Explanation:

Given that the average of 5 numbers is 7. So you have to find the total values of 5 numbers :

`let \: x = total \: values`

`(x)/(5) = 7`

`x = 7 * 5`

`x = 35`

Assuming that the total values of 5 numbers is 35. Next, we have to find the removed number :

`let \: y = removed \: number`

`(35 - y)/(4) = 6`

`35 - y = 6 * 4`

`35 - y = 24`

`35 - 24 = y`

`y = 11`