Answer:
The triangle is not equilateral.
Explanation:
Distance formula:

Distance from (a, a) to (-a, -a):
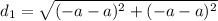
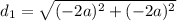

Distance from (-a, -a) to (-3a, 3a):
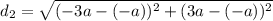

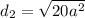
Distance from (-3a, 3a) to (a, a):
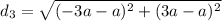
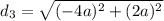
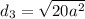
The three sides do not have the same length, so the triangle is not equilateral.