Answer
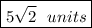
Step by step explanation
Let the points be A and B
A ( - 3 , - 4 ) ⇒( x₁ , y₁ )
B ( 4 , - 5 )⇒( x₂ , y₂ )
Now, let's find the distance between these points :
Distance =
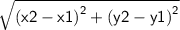
Plug the values
⇒
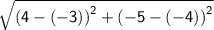
Calculate
⇒
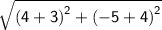
⇒
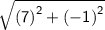
Evaluate the power
⇒
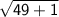
Add the numbers
⇒
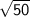
Simplify the radical expression
⇒
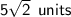
Hope I helped!
Best regards!!