Question

the angle of elevation of the top of a tower from a point 42m away from the base on level ground is 36 find the height of the tower​

Answer 1

30.51 meters

Explanation:

Given that:

The distance from the point to the base of the tower = 42 m, the angle of elevation = 36°.

According to sine rule if a,b,c are the sides of a triangle and its respective opposite angles are A, B, C. Therefore:

`(a)/(sin(A)) =(b)/(sin(B))=(c)/(sin(C))`

Let the height of the tower be a and the angle opposite the height be A = angle of elevation = 36°

Also let the distance from the point to the base of the tower be b = 42 m, and the angle opposite the base of the tower be B

To find B, since the angle between the height of the tower and the base is 90°, we use:

B + 36° + 90° = 180° (sum of angles in a triangle)

B + 126 = 180

B = 180 - 126

B = 54°

Therefore using sine rule:

`(a)/(sin(A)) =(b)/(sin(B))\\\\(a)/(sin(36))=(42)/(sin(54))\\\\ a=(42*sin(36))/(sin(54))\\ \\a=30.51\ meters`

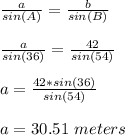
The height of the tower is 30.51 meters