Question

Triangle A' B' C' is a dilation of a triangle ABC. The scale factor is
`(3)/(4)`. Point B is 11 inches away from the center of dilation is point B'?

Answer 1

None of the options are correct

Explanation:

Let us assume point B is at (x, y) and the center of dilation is at (a, b). Therefore the distance between the two points is:

`Distance =√((b-y)^2+(a-x)^2)=11 \\\\√((b-y)^2+(a-x)^2)=11`

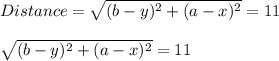
If Triangle ABC is then dilated by 3/4, the new coordinate is B'(3/4 (x-a) + a, 3/4 (y - b) + b). The distance between B' and the center of dilation would be:

`Distance =\sqrt{(b-[(3)/(4)( y-b)+b])^2+(a-[(3)/(4) (x-a)+a])^2}`

Therefore the distance cannot be gotten until the center of dilation is given