Question

Use the discriminant to determine the number of real solutions to the equation. −4x^2=−8−10x

Answer 1

4

Explanation:

Answer 2

Explanation:

You don't get a free answer. I am, after all, a high school math teacher, so there has to be a lesson in with this.

The discriminant is part of the quadratic formula. It is:

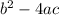`b^2-4ac`. If this value is found to be > 0 and a perfect square, there are 2 real roots; if this value is found to >0 and not a perfect square, there are 2 complex roots; if this value is found to be = 0, then there is 1 real root with a multiplicity of 2; and finally, if this value is found to be < 0, then there are 2 imaginary roots. Also, it would help to know that, because we are dealing with the discriminant, which comes from the quadratic formula, and quadratics, by definition, have 2 solutions, you must have 2 solutions listed as the possible roots for the equation. Our equation is:

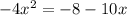`-4x^2=-8-10x` but in order to determine the a, b, and c for the discriminant, that equation has to be in standard form, set equal to 0:

`-4x^2+10x+8=0`

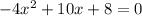
From this we can see that a = -4, b = 10, and c = 8. Filling in the discriminant:

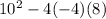`10^2-4(-4)(8)` which gives us a value of

100 - [4(-4)(8)] (don't forget orders of operation here!)

100 - (-128) = 100 + 128 = 228

This value is greater than 0 but is not a perfect square, so there are 2 complex roots. That means that there will be radicals in the solutions.