Question

For the given graph, a. describe the end behavior,

b. determine whether it represents an odd-degree or even-degree polynomial function, and
c. state the number of real zeros.

Answer 1

See below.

Explanation:

A)

The end behavior is basically how the function behaves as it approaches negative or positive infinity.

As the function approaches negative infinity, we can see that the graph is going up. In other words:

`f(x)\rightarrow\infty\text{ as }x\rightarrow-\infty`

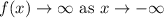
As the function approaches positive infinity, we can see that the graph is going down. In other words:

`f(x)\rightarrow-\infty\text{ as }x\rightarrow\infty`

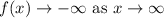
B)

In even-degree polynomials, both ends of the graph will be going the same way. In this graph, the two ends are going opposite ways so this is an odd-degree function.

C)

The number of real zeros is simply the amount of times the graph crosses the x-axis. In the graph, the function does this three times. Thus, the number of real zeros is 3.