Answer:
Explanation:
A fifth-grade polynomial requires a minimum of 6 different points to create an adequate graph. Let is
 the dominion of the polynomial, such that
the dominion of the polynomial, such that
 ,
,
 ,
,
 ,
,
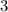 ,
,
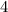 ,
,

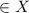 . The values of the function for each value are calculated herein:
. The values of the function for each value are calculated herein:
x = 0
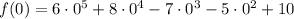
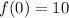
x = 1
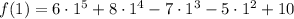
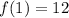
x = 2
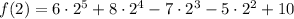

x = 3

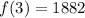
x = 4
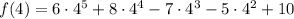
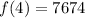
x = 5
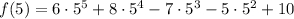

The table is now presented:
x y
0 10
1 12
2 254
3 1882
4 7674
5 22760
Finally, the graphic is now constructed by using an online tool (i.e. Desmos). The image is included below as attachment.