Question

A golfer hits a 42 g ball, which comes down on a tree root and bounces straight up with an initial speed of 15.6 m/s. Determine the height the ball will rise after the bounce. Show all your work.

Answer 1

12.2 m

Step-by-step explanation:

Given:

v₀ = 15.6 m/s

v = 0 m/s

a = -10 m/s²

Find: Δy

v² = v₀² + 2aΔy

(0 m/s)² = (15.6 m/s)² + 2 (-10 m/s²) Δy

Δy = 12.2 m

Answer 2

`\LARGE{ \boxed{ \rm{ \green{Answer:}}}}`

Given,

• The initial speed is 15.6 m/s
• The mass of the ball is 42g = 0.042kg

Finding the initial kinetic energy,

`\large{ \boxed{ \rm{K.E. = (1)/(2)m {v}^(2)}}}`

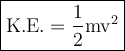
⇛ KE = (1/2)mv²

⇛ KE = (1/2)(0.042)(15.6)²

⇛ KE = 5.11 J

|| ⚡By conservation of energy, the potential energy at the highest point will also be 5.11 J, since there is no kinetic energy at the highest point because the ball is not moving (we neglect energy lost due to air resistance, heat, sound, etc.) ⚡||

So, we have:

`\large{ \boxed{ \rm{P.E. = mgh}}}`

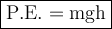
⇛ h = PE/(mg)

⇛ h = 5.11 J /(0.042 × 9.8)

⇛ h = 12.41 m

✏The ball will rise upto a height of 12.41 m

━━━━━━━━━━━━━━━━━━━━