Question

In recent years, the interest rates on home mortgages have declined to less than 6%. However, a

recent study shows that the rate charged on credit card debt is more than 14%. A sample of 10 credit
cards showed that the mean rate charged is 15.64% with a standard deviation of 1.561%. At 1% level
of significance, is it reasonable to conclude the mean rate charged is greater than 14%?

Answer 1

Yes it is reasonable to conclude the mean rate charged is greater than 14%

Explanation:

From the question we are told that

The population mean is
`\mu = 0.14`

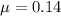
The sample size is
`n = 10`

The sample mean is
`\= x = 0.1564`

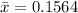
The standard deviation is
`\sigma = 0.01561`

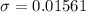
The level of significance is
`\alpha = 0.01`

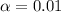
The null hypothesis is
`H_o: \mu = 0.14`

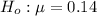
The alternative hypothesis is
`H_a : \mu > 0.14`

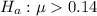
Generally the test statistic is mathematically represented as

`t = ( \= x - \mu )/( (\sigma )/(√(n) ) )`

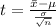
substituting values

`t = ( 0.1564 - 0.14 )/( (0.01561 )/(√(10) ) )`

`t = 3.322`

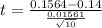
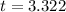
Now the p-value obtained from the z-table is

`p-value = P(t > 3.322) = 0.00044687`

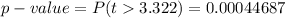
Since the
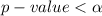`p-value < \alpha` then we reject the null hypothesis, hence we can conclude that the mean rate charged is greater than 14%