Answer:
Yes it is reasonable to conclude the mean rate charged is greater than 14%
Explanation:
From the question we are told that
The population mean is
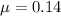
The sample size is

The sample mean is
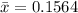
The standard deviation is
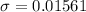
The level of significance is

The null hypothesis is
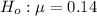
The alternative hypothesis is
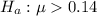
Generally the test statistic is mathematically represented as

substituting values
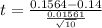
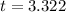
Now the p-value obtained from the z-table is

Since the
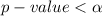 then we reject the null hypothesis, hence we can conclude that the mean rate charged is greater than 14%
then we reject the null hypothesis, hence we can conclude that the mean rate charged is greater than 14%