Answer:
0
Explanation:
Hello, please consider the following.
For any a and b real numbers we can write.
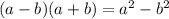
We apply this formula two times here, as below.
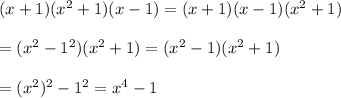
We have the coefficient of 1 for
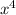 and the constant term is -1, so the sum of the coefficients is 0.
and the constant term is -1, so the sum of the coefficients is 0.
Thank you.