Answer:
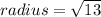 or
or
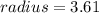
Explanation:
Given
Points:
A(-3,2) and B(-2,3)
Required
Determine the radius of the circle
First, we have to determine the center of the circle;
Since the circle has its center on the x axis; the coordinates of the center is;
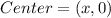
Next is to determine the value of x through the formula of radius;
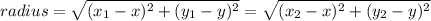
Considering the given points
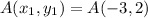
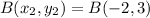
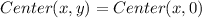
Substitute values for
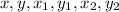 in the above formula
in the above formula
We have:
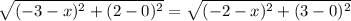
Evaluate the brackets
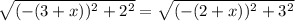
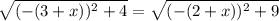
Eva;uate all squares
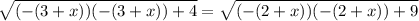
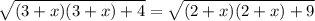
Take square of both sides
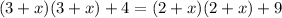
Evaluate the brackets
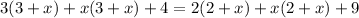
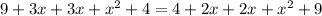
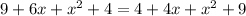
Collect Like Terms
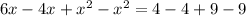
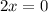
Divide both sides by 2
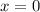
This implies the the center of the circle is
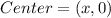
Substitute 0 for x
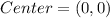
Substitute 0 for x and y in any of the radius formula
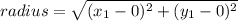
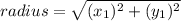
Considering that we used x1 and y1;
In this case we have that;
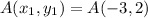
Substitute -3 for x1 and 2 for y1
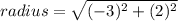
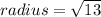
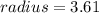 ---Approximated
---Approximated