Answer:
1)
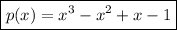
2)

3)
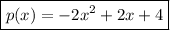
4)

Explanation:
Part (1)
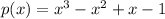
As we have to determine it by ourselves, this is the polynomial having a degree of 3. p(x) with a degree of 3 means that the highest degree/exponent of x should be 3.
Part (2)
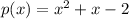
This can be the polynomial having the factor x-1 because if we put:
x - 1 = 0 => x = 1 in the above polynomial, it gives us a result of zero which shows us that (x-1) "is" a factor of the polynomial.
Part (3)
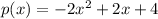
This can be the polynomial for which p(0) = 4 and p(-1) = 0
Let's check:


So, this is the required polynomial determined by "myself".
Part (4):

This is the polynomial having a remainder 6 when divided by (x-2)
Let's check:
Let x - 2 = 0 => x = 2
Putting in the above polynomial
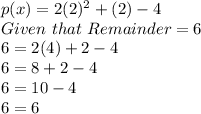
So, Proved that it has a remainder of 6 when divided by (x-2)