Question

Solve the triangle. A = 51°, b = 14, c = 6

Answer 1

Answer: a = 11.24 B = 75.5° C = 53.5°

Explanation:

Use Law of Cosines to find a: a² = b² + c² - 2bc · cos A

Given: b = 14, c = 6, A = 51°

a² = (14)² + (6)² - 2(14)(6) · cos 51°

a² = 196 + 36 - 168 · cos 51°

a² = 232 - 105.72

a² = 126.27

a = 11.24

Use Law of Sines to find B:
`(\sin A)/(a)=(\sin B)/(b)`

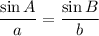
Given: A = 51°, a = 11.24, b = 14

`(\sin 51^o)/(11.24)=(\sin B)/(14)\\\\\\(14\sin51^o)/(11.24)=\sin B\\\\\\\sin^(-1)\bigg((14\sin51^o)/(11.24)\bigg)=B\\\\\\75.5^0=B`

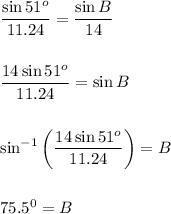
Use Triangle Sum Theorem to find C: A + B + C = 180°

Given: A = 51°, B = 75.5°

51° + 75.5° + C = 180°

126.5° + C = 180°

C = 53.5°