Answer:
The answer is option B
Explanation:
To find the coefficient of the third term in
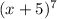
Rewrite the expansion in the form

where n is the index
So we have

After that we use the formula
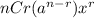
where r is the term we are looking for
For the third term we are looking for the term containing x²
that's
r + 1 = 3
r = 2
So to find the coefficient of the third term
We have
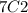
Hope this helps you