Question

The equation represents the decomposition of a generic diatomic element in its standard state. 12X2(g)⟶X(g) Assume that the standard molar Gibbs energy of formation of X(g) is 4.25 kJ·mol−1 at 2000. K and −63.12 kJ·mol−1 at 3000. K. Determine the value of K (the thermodynamic equilibrium constant) at each temperature.

Answer 1

`K^(2000K)=0.774\\\\K^(3000K)=12.56`

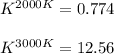
Step-by-step explanation:

Hello,

In this case, considering the reaction, we can compute the Gibbs free energy of reaction at each temperature, taking into account that the Gibbs free energy for the diatomic element is 0 kJ/mol:

`\Delta _rG=\Delta _fG_(X)-(1)/(2) \Delta _fG_(X_2)=\Delta _fG_(X)`

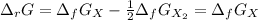
Thus, at 2000 K:

`\Delta _rG=\Delta _fG_(X)^(2000K)=4.25kJ/mol`

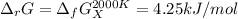
And at 3000 K:

`\Delta _rG=\Delta _fG_(X)^(3000K)=-63.12kJ/mol`

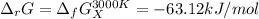
Next, since the relationship between the equilibrium constant and the Gibbs free energy of reaction is:

`K=exp(-(\Delta _rG)/(RT) )`

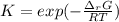
Thus, at each temperature we obtain:

`K^(2000K)=exp(-(4250J/mol)/(8.314(J)/(mol* K)*2000K) )=0.774\\\\K^(3000K)=exp(-(-63120J/mol)/(8.314(J)/(mol* K)*3000K) )=12.56`

In such a way, we can also conclude that at 2000 K reaction is unfavorable (K<1) and at 3000 K reaction is favorable (K>1).

Best regards.