Answer:
At the 5% level, BAOI can infer that the average time to complete does not exceeds 60 hours.
Explanation:
From the question we are told that
The population mean is

The sample size is

The sample mean is
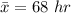
The standard deviation is

The null hypothesis is
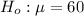
The alternative
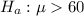
Here we would assume the level of significance of this test to be
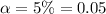
Next we will obtain the critical value of the level of significance from the normal distribution table, the value is
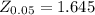
Generally the test statistics is mathematically represented as
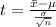
substituting values
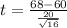
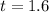
Looking at the value of t and
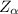 we see that
we see that
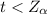 hence we fail to reject the null hypothesis
hence we fail to reject the null hypothesis
This means that there no sufficient evidence to conclude that it takes more than 60 hours to complete the course
So
At the 5% level, BAOI can infer that the average time to complete does not exceeds 60 hours.