Answer:
The z-score for 1880 is 1.34.
The z-score for 1190 is -0.88.
The z-score for 2130 is 2.15.
The z-score for 1350 is -0.37.
And the z-score of 2130 is considered to be unusual.
Explanation:
The complete question is: A standardized exam's scores are normally distributed. In recent years, the mean test score was 1464 and the standard deviation was 310. The test scores of four students selected at random are 1880, 1190, 2130, and 1350. Find the z-scores that correspond to each value and determine whether any of the values are unusual. The z-score for 1880 is nothing. (Round to two decimal places as needed.) The z-score for 1190 is nothing. (Round to two decimal places as needed.) The z-score for 2130 is nothing. (Round to two decimal places as needed.) The z-score for 1350 is nothing. (Round to two decimal places as needed.) Which values, if any, are unusual? Select the correct choice below and, if necessary, fill in the answer box within your choice. A. The unusual value(s) is/are nothing. (Use a comma to separate answers as needed.) B. None of the values are unusual.
We are given that the mean test score was 1464 and the standard deviation was 310.
Let X = standardized exam's scores
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean test score = 1464
= mean test score = 1464
 = standard deviation = 310
= standard deviation = 310
S, X ~ Normal(
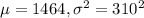 )
)
Now, the test scores of four students selected at random are 1880, 1190, 2130, and 1350.
So, the z-score of 1880 =

=
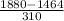 = 1.34
= 1.34
The z-score of 1190 =

=
 = -0.88
= -0.88
The z-score of 2130 =

=
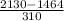 = 2.15
= 2.15
The z-score of 1350 =

=
 = -0.37
= -0.37
Now, the values whose z-score is less than -1.96 or higher than 1.96 are considered to be unusual.
According to our z-scores, only the z-score of 2130 is considered to be unusual as all other z-scores lie within the range of -1.96 and 1.96.