Question

A 3200-lb car is moving at 64 ft/s down a 30-degree grade when it runs out of fuel. Find its velocity after that if friction exerts a resistive force with magnitude proportional to the square of the speed with k

Answer 1

The velocity is 40 ft/sec.

Step-by-step explanation:

Given that,

Force = 3200 lb

Angle = 30°

Speed = 64 ft/s

The resistive force with magnitude proportional to the square of the speed,

`F_(r)=kv^2`

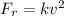
Where, k = 1 lb s²/ft²

We need to calculate the velocity

Using balance equation

`F\sin\theta-F_(r)=m(d^2v)/(dt^2)`

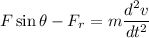
Put the value into the formula

`3200\sin 30-kv^2=m(d^2v)/(dt^2)`

Put the value of k

`3200*(1)/(2)-v^2=m(d^2v)/(dt^2)`

`1600-v^2=m(d^2v)/(dt^2)`

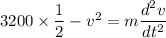
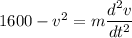
At terminal velocity
`(d^2v)/(dt^2)=0`

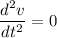
So,
`1600-v^2=0`

`v=√(1600)`

`v=40\ ft/sec`

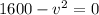
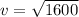
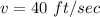
Hence, The velocity is 40 ft/sec.