Question

Hydrazine, , emits a large quantity of energy when it reacts with oxygen, which has led to hydrazine used as a fuel for rockets: How many moles of each of the gaseous products are produced when 20.1 g of pure hydrazine is ignited in the presence of 20.1 g of pure oxygen

Answer 1

`1.25~mol~H_2O` and
`0.627~mol~N_2`

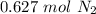
Step-by-step explanation:

Our goal for this question is the calculation of the number of moles of the molecules produced by the reaction of hydrazine (
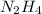`N_2H_4`) and oxygen (
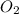`O_2`). So, we can start with the reaction between these compounds:

`N_2H_4~+~O_2~->~N_2~+~H_2O`

Now we can balance the reaction:

`N_2H_4~+~O_2~->~N_2~+~2H_2O`

In the problem, we have the values for both reagents. Therefore we have to calculate the limiting reagent. Our first step, is to calculate the moles of each compound using the molar masses values (32.04 g/mol for
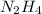`N_2H_4` and 31.99 g/mol for
`O_2`):

`20.1~g~N_2H_4(1~mol~N_2H_4)/(32.04~g~N_2H_4)=0.627~mol~N_2H_4`

`20.1~g~O_2(1~mol~O_2)/(31.99~g~O_2)=0.628~mol~O_2`

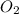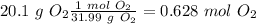
In the balanced reaction we have 1 mol for each reagent (the numbers in front of
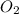`O_2` and
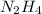`N_2H_4` are 1). Therefore the smallest value would be the limiting reagent, in this case, the limiting reagent is
`N_2H_4`.

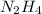With this in mind, we can calculate the number of moles for each product. In the case of
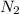`N_2` we have a 1:1 molar ratio (1 mol of
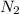`N_2` is produced by 1 mol of
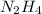`N_2H_4`), so:

`0.627~mol~N_2H_4(1~mol~N_2)/(1~mol~N_2H_4)=~0.627~mol~N_2`

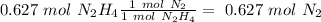
We can follow the same logic for the other compound. In the case of
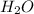`H_2O` we have a 1:2 molar ratio (2 mol of
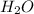`H_2O` is produced by 1 mol of
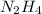`N_2H_4`), so:

`0.627~mol~N_2H_4(2~mol~H_2O)/(1~mol~N_2H_4)=~1.25~mol~H_2O`

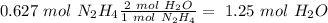
I hope it helps!